1. Phương pháp mặt trượt trụ tròn
Phương phát mặt trượt trụ tròn được ứng dụng để tính toán ổn định mái dốc khi: Mái dốc đồng nhất, cấu tạo từ đất dính với giả thiết khi mất ổn định mái dốc sẽ trượt theo mặt trượt trụ tròn hoặc gần giống trụ tròn.
Như vật, để có thể dự đoán được mức độ ổn định cơ học của sườn dốc, trong mọi trường hợp đền cần phải điều tra xác định được: vị trí tương đối chính xác (hoặc tương đối hợp lý) của mặt trượt, các chỉ tiêu cơ lý của đất (c, ø, γ) ở trạng thái tính toán (tương ứng với độ chứa ẩm bất lợi nhất).

2. Phương pháp Fellenius
Fellenius đưa ra giả thiết: Khi trượt, cả khối trượt sẽ cùng trượt một lúc. Do đó giữa các mảnh không có lực ngang tác dụng lên nhau, trạng thái giới hạn chỉ xảy ra trên mặt trượt.
3. Phương pháp Bishop
Về nguyên tắc, phương pháp Bishop tương tự như phương pháp Fellenius, chỉ khác là ở mỗi mảnh trượt Bishop có xét thêm lực tương tác giữa các mặt đứng của phân mảnh trượt (không quan tâm đến vị trí của điểm đặt của các lực này).

Nếu xét các lực trên thì phương pháp này rất phức tạp. Nhằm đơn giản hoác, Bishop đã giả thiết các lực Vi+1 = Vi-1 và khi ở trạng thái cân bằng thì:

4. Phần mềm Geo – Slope/W
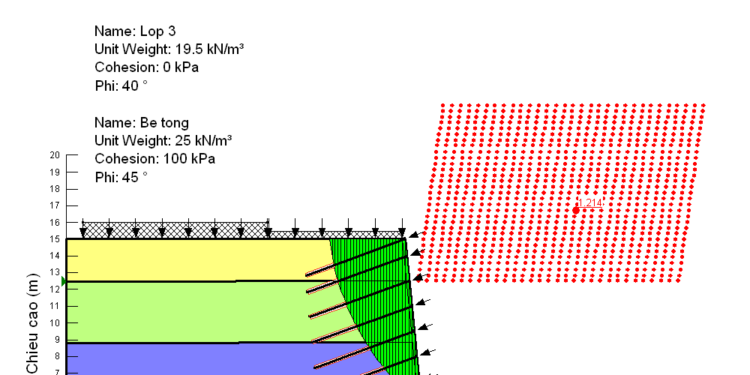
Bộ phần mềm Geo – Slope (Canada): được nhiều nước trên thế giới đánh giá là bộ chương trình mạnh nhất, được dùng phổ biến nhất hiện nay. Trong phạm vi đồ án, sử dụng phần mềm Geo – Slope/W để phân tích ổn định mái dốc, mái dốc có gia cường.
Trong mọi trường hợp, các yêu cầu của nền đường được thể hiện một các định lượng qua hệ số ổn định toàn khối Kođ.
+ Hệ số ổn định Kođ < 1 thì nền thiếu ổn định.
+ Hệ số ổn định Kođ >= 1 thì nền đạt đủ điều kiện ổn định.
+ Hệ số ổn định Kođ thường thay đổi từ 1.0 – 1.5.
+ Sử dụng phần mềm Geo – Slope/W để phân tích ổn định mái dốc, tính toán hệ số Kođ từ đó đánh giá được độ ổn định của nền.

5. Phương pháp phần tử hữu hạn
Phương pháp phần tử hữu hạn là phương pháp số gần đúng để giải các bài toán được mô tả bởi các phương trình vi phân đạo hàm riêng trên miền xác định có hình dạng và điều kiện biên bất kỳ mà nghiệm chính xác không thể tìm được bằng phương pháp giải tích.
Cơ sở của phương pháp này là làm rời rạc hóa miền xác định của bài toán, bằng cách chia nó thành nhiều miền con (phần tử). Các phần tử này được liên kết với nhau tại các điểm nút chung. Trong phạm vi của mỗi phần tử Nghiệm được chọn là một hàm số nào đó được xác định thông qua các giá trị chưa biết tại các điểm nút của phần tử gọi là hàm xấp xỉ thoả mãn điều kiện cân bằng của phần tử. Tập tất cả các phần tử có chú ý đến điều kiện liên tục của sự biến dạng và chuyển vị tại các điểm nút liên kết giữa các phần tử. Kết quả đẫn đến một hệ phương trình đại số tuyến tính mà ẩn số chính là các giá trị của hàm xấp xỉ tại các điểm nút. Giải hệ phương trình này sẽ tìm được các giá trị của hàm xấp xỉ tại các điểm nút của mỗi phần tử, nhờ đó hàm xấp xỉ hoàn toàn được xác định trên mỗi một phần tử.
6. Phần mềm Plaxis
Phần mềm Plaxis là sản phẩm của Đại học công nghệ Delf – Hà Lan và được công ty Plaxis BV phát triển theo các chủ đề riêng, được viết dựa trên phương pháp phần tử hữu hạn phân tích bài toán cơ học đất, là tiến hành chia công trình có kết cấu liền khối thành nhiều phần tử hữu hạn liên kết tương hỗ trên các điểm nút, các phần tử này gọi là phần tử hữu hạn.

Plaxis là phần mềm phần tử hữu hạn mạnh mẽ trong mô hình, phân tích ổn định biến dạng trong kết cấu đất và đá. Phần mềm được sử dụng rộng rãi trên toàn cầu bới các công ty địa kỹ thuật, các viện nghiên cứu địa kỹ thuật và ngành xây dựng công trình ngầm. Ứng dụng trong các bài toán: đào đất, đắp đất, hố đào sâu, đường hầm, ứng dụng trong khai khoáng và môi trường…
Cơ sở lý thuyết giải bài toán phần tử hữu hạn trong phần mềm Plaxis theo 6 bước sau:
+ Chia miền phân tích các phần tử đơn;
+ Chọn hàm xấp xỉ thích hợp;
+ Xây dựng phương trình phần tử, hay thiết lập ma trận độ cứng phần tử và véc tơ tải trọng;
+ Ghép nối các phần tử trên cơ sở mô hình tương thích mà kết quả là hệ thống phương trình;
+ Tìm nghiệm của phương trình cân bằng điểm nút, dùng điều kiện biên chuyển dịch hoặc rằng buộc chuyển dịch để tìm nghiệm của phương trình cân bằng điểm nút, từ đó ta được chuyển dịch của điểm nút;
+ Tính giá trị các đại lượng ứng suất, biến dạng, chuyển dịch của các phần tử đơn.